Values of π(x) and Δ(x) for various x's

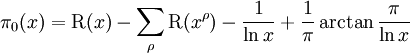
The tables were compiled by Andrey V. Kulsha. See below the explanation of Δ(x).

Values of x	Tables	Local minima of Δ(x)	Local maxima of Δ(x)
From 1 to 10 with a step of 0.0001	1e01.txt	Δ(5-0) = -0.3952461978	Δ(1+0) = +1.0000000000
From 10¹ to 10² with a step of 0.001	1e02.txt	Δ(11-0) = -0.5492343329	Δ(19+0) = +0.5607597113
From 10² to 10³ with a step of 0.01	1e03.txt	Δ(223-0) = -0.6051733874	Δ(113+0) = +0.7848341482
From 10³ to 10⁴ with a step of 0.1	1e04.txt	Δ(1423-0) = -0.7542604400	Δ(1627+0) = +0.6754517455
From 10⁴ to 10⁵ with a step of 1	1e05.txt	Δ(19373-0) = -0.7278356754	Δ(24137+0) = +0.7457431860
From 10⁵ to 10⁶ with a step of 10¹	1e06.txt	Δ(302831-0) = -0.6995719492	Δ(355111+0) = +0.7008073861
From 10⁶ to 10⁷ with a step of 10²	1e07.txt	Δ(1090697-0) = -0.6389660809	Δ(3445943+0) = +0.6809987397
From 10⁷ to 10⁸ with a step of 10³	1e08.txt	Δ(36917099-0) = -0.7489165055	Δ(30909673+0) = +0.7157292126
From 10⁸ to 10⁹ with a step of 10⁴	1e09.txt	Δ(516128797-0) = -0.6775687236	Δ(110102617+0) = +0.7878100197
From 10⁹ to 10¹⁰ with a step of 10⁵	1e10.txt	Δ(7712599823-0) = -0.6889577485	Δ(1110072773+0) = +0.6833192028
From 10¹⁰ to 10¹¹ with a step of 10⁶	1e11.txt	Δ(11467849447-0) = -0.7251609705	Δ(10016844407+0) = +0.6386706267
From 10¹¹ to 10¹² with a step of 10⁷	1e12.txt	Δ(110486344211-0) = -0.7355462679	Δ(330957852107+0) = +0.7533813432
From 10¹² to 10¹³ with a step of 10⁸	1e13.txt	Δ(1635820377397-0) = -0.6892596608	Δ(2047388353069+0) = +0.6808028098
From 10¹³ to 10¹⁴ with a step of 10⁹	1e14.txt	Δ(36219717668609-0) = -0.8360329846	Δ(21105695997889+0) = +0.6896466780
From 10¹⁴ to 10¹⁵ with a step of 10¹⁰	1e15.txt	Δ(348323506633621-0) = -0.6494959371	Δ(117396942462053+0) = +0.6789107425
From 10¹⁵ to 10¹⁶ with a step of 10¹¹	1e16.txt*	Δ(1212562524413153-0) = -0.7750460589	Δ(1047930291039067+0) = +0.7042622330
From 10¹⁶ to 10¹⁷ with a step of 10¹³	1e17.txt**	Δ(18019655286689201-0) = -0.5710665212	Δ(16452596773450799+0) = +0.7144542025
From 10¹⁷ to 10¹⁸ with a step of 10¹⁴	1e18.txt**	Δ(266175790131587543-0) = -0.7599282036	Δ(125546149553907317+0) = +0.6572554320
From 10¹⁸ to 10¹⁹ with a step of 10¹⁵	1e19.txt**	(to be computed)	(to be computed)
From 10¹⁹ to 10²⁰ with a step of 10¹⁶ (should be completed for x > 5.675e19)	1e20.txt**	(to be computed)	(to be computed)
10²⁰ and larger	large.txt**	Δ(x) has no global minimum	Δ(x) has no global maximum

*The values of π(x) were computed by Anatoly F. Selevich.
**The values of π(x) were taken from [1] except the value of π(1.5·10²²) from [2].

Some extreme regions where |Δ(x)| exceeds 0.75

Values of x	Tables	# of entries
From 1.100·10⁸ to 1.102·10⁸ with a step of 10¹	1e09_max.txt	20 001
From 3.309·10¹¹ to 3.310·10¹¹ with a step of 10⁴	1e12_max.txt	10 001
From 3.309578·10¹¹ to 3.309580·10¹¹ with a step of 10¹	1e12_max2.txt	20 001
From 3.590·10¹³ to 3.625·10¹³ with a step of 10⁷	1e14_min.txt	35 001
From 3.62194·10¹³ to 3.62200·10¹³ with a step of 10⁴	1e14_min2.txt	60 001
From 3.62197176·10¹³ to 3.62197178·10¹³ with a step of 10¹	1e14_min3.txt	20 001
From 1.212·10¹⁵ to 1.214·10¹⁵ with a step of 10⁹	1e16_min.txt	2 001
From 1.21255·10¹⁵ to 1.21257·10¹⁵ with a step of 10⁶	1e16_min2.txt	20 001
From 1.212562517·10¹⁵ to 1.212562526·10¹⁵ with a step of 10²	1e16_min3.txt	90 001
From 3.294·10¹⁵ to 3.297·10¹⁵ with a step of 10⁹	1e16_min_.txt	3 001
From 2.6615·10¹⁷ to 2.6635·10¹⁷ with a step of 10¹²	1e18_min.txt	201
From 2.661751·10¹⁷ to 2.661760·10¹⁷ with a step of 10⁷	1e18_min2.txt	90 001
From 2.6617579011·10¹⁷ to 2.6617579017·10¹⁷ with a step of 10³	1e18_min3.txt	60 001

These results confirm some previously made computations [3] [4]. See also [5] and [6] about the oscillations of π(x) at larger x's.

Where did Δ(x) come from?

The prime-counting function, π(x), may be computed analytically. The explicit formula for it, valid for x > 1, looks like

$\pi_{0}(x) = \operatorname{R}(x) - \sum_{\rho}\operatorname{R}(x^{\rho}) - \frac{1}{\ln x} + \frac{1}{\pi} \arctan \frac{\pi}{\ln x}$

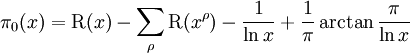
where

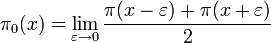
$\pi_{0}(x) = \lim_{\varepsilon \rightarrow 0}\frac{\pi(x-\varepsilon)+\pi(x+\varepsilon)}{2}$

$\operatorname{R}(x^\rho) = 1 + \sum_{k=1}^\infty \frac{(\rho \ln x)^k}{k! k \zeta(k+1)}$

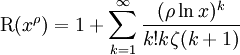
and the sum runs over the non-trivial (i.e. with positive real part) roots of Riemann ζ-function in order of increasing the absolute value of the imaginary part. This sum describes the fluctuations of π(x), while the remaining terms give the «smooth» part of it and may be used as a very good estimator of π(x):

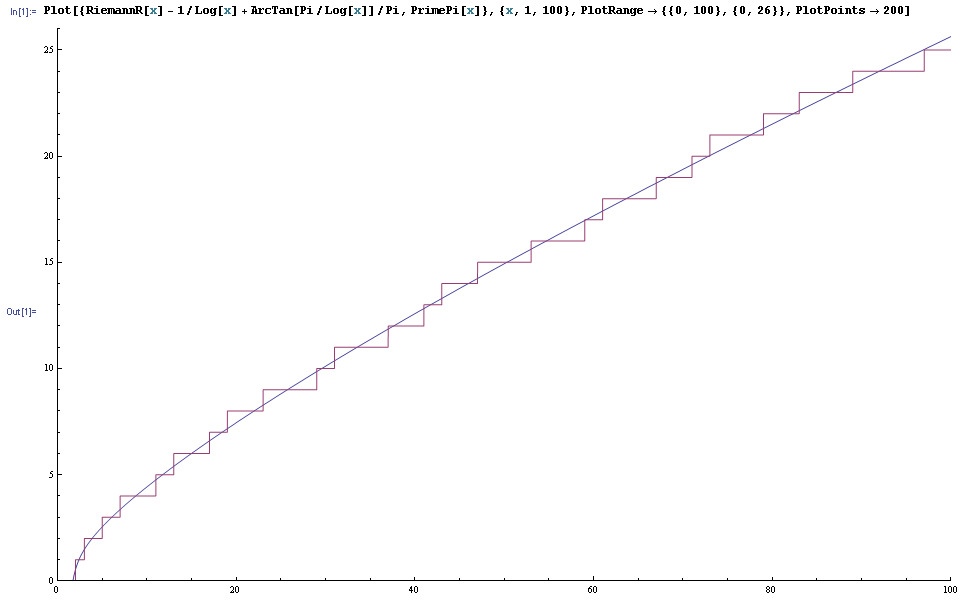
The smooth part of Pi(x)

Here you can see the plot of π(x) (the purple line) compared to the blue line of

$\operatorname{R}(x) - \frac{1}{\ln x} + \frac{1}{\pi} \arctan \frac{\pi}{\ln x}$

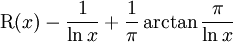
The difference between these two heuristically oscillates with an amplitude of about

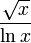
$\frac{\sqrt x}{\ln x}$

so we have the following expression for Δ(x), the function which clearly represents the fluctuations of the distribution of primes:

$\Delta(x) = \left( \pi_{0}(x) - \operatorname{R}(x) + \frac{1}{\ln x} - \frac{1}{\pi}\arctan \frac{\pi}{\ln x} \right) \frac{\ln x}{\sqrt x}$

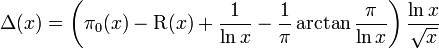
There's a plot of Δ(x) on the log scale:

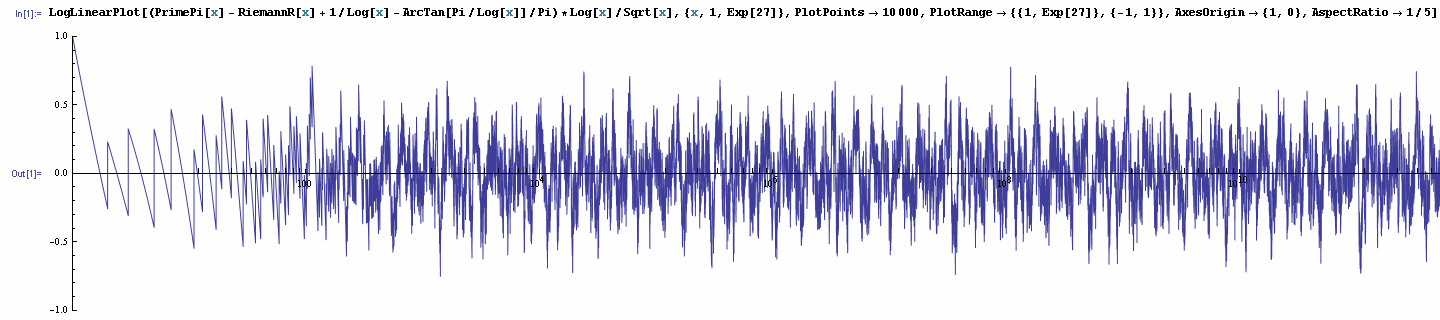
Delta(x) on the log scale

On the explicit formula for π(x)

Curiously, this formula seems to be never seen in literature [7], so let's describe its origin. The formula comes from the Möbius inversion

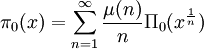
$\pi_{0}(x) = \sum_{n=1}^{\infty} \frac{\mu(n)}{n} \Pi_{0}(x^{\frac{1}{n}})$

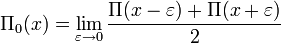
$\Pi_{0}(x) = \lim_{\varepsilon \rightarrow 0}\frac{\Pi(x-\varepsilon)+\Pi(x+\varepsilon)}{2}$

where

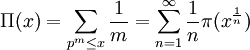
$\Pi(x) = \sum_{p^n \le x} \frac{1}{n} = \sum_{n=1}^{\infty} \frac{1}{n} \pi(x^{\frac{1}{n}})$

is so-called Riemann prime-counting function (the first sum runs over the powers of primes). We have the following expression for Π₀(x) [8]:

$\Pi_{0}(x) = \operatorname{li}(x) - \sum_{\rho}\operatorname{li}(x^{\rho}) - \ln 2 + \int_x^\infty \frac{dt}{t(t^2-1) \ln t}$

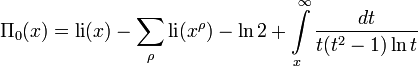
where li is the logarithmic integral; li(x^ρ) should be considered as Ei(ρlnx), where Ei is the analytic continuation of the exponential integral function from positive reals to the complex plane with branch cut along the negative reals. The sum runs, as before, over the non-trivial roots of ζ-function in the same manner. Thus, we have

$\sum_{n=1}^{\infty} \frac{\mu(n)}{n} = 0$

$\sum_{n=1}^{\infty} \frac{\mu(n)}{n} \operatorname{li}(x^{\frac{1}{n}}) = \operatorname{R}(x)$

$\sum_{n=1}^{\infty} \frac{\mu(n)}{n} \int_{\frac{\ln x}{n}}^{\infty} \frac{dt}{(e^{2t}-1)t} = \frac{1}{\pi} \arctan \frac{\pi}{\ln x} - \frac{1}{\ln x}$

$\sum_{n=1}^{\infty} \frac{\mu(n)}{n} \left( \sum_{\rho}\operatorname{li}(x^{\frac{\rho}{n}}) - \frac{n}{2 \ln x} \right) = \sum_{\rho}\operatorname{R}(x^{\rho}) + \frac{1}{\ln x}$

and the formula immediately follows.

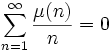
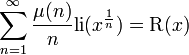
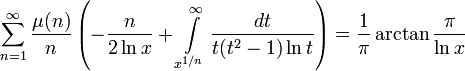
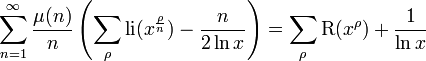
P.S. The first two equalities are well-known [8]; the third one comes straightly from the (32) in [9], while the last one is based on the identity

$\lim_{t\rightarrow\infty}\sum_{n=1}^{\infty}\mu(n)\left(\frac{u}{n}\sum_{|\operatorname{Im}(\rho)|>t}\operatorname{Ei}\left(\rho\frac{u}{n}\right)-\frac12\right) \equiv 1$

which holds for u > 0.

References

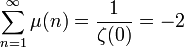
[1] Tomás Oliveira e Silva. Tables of values of pi(x) and of pi2(x). http://www.ieeta.pt/~tos/primes.html

[2] Xavier Gourdon. Counting the number of primes. http://numbers.computation.free.fr/Constants/Primes/countingPrimes.html

[3] Nuna da Costa Pereira. Computational results on some prime number functions. http://mat.fc.ul.pt/ind/ncpereira/

[4] Tadej Kotnik. The prime-counting function and its analytic approximations. Adv. Comp. Math., Vol. 29, N. 1 (2008), pp. 55-70.

[5] Kuok Fai Chao, Roger Plymen. A new bound for the smallest $x$ with $\pi(x) > li(x)$. http://arxiv.org/abs/math/0509312

[6] Patrick Demichel. The prime counting function and related subjects. http://demichel.net/patrick/li_crossover_pi.pdf

[7] Jonathan M. Borwein, David M. Bradley, Richard E. Crandall. Computational strategies for the Riemann zeta function. J. Comp. App. Math., Vol. 121 (2000), pp. 247-296.

[8] H.M. Edwards. Riemann's Zeta Function. Academic Press, 1974

[9] Hans Riesel, Gunnar Gohl. Some Calculations Related to Riemann's Prime Number Formula. Math. Comp., Vol. 24, N. 112 (1970), pp. 969-983

updated on Tuesday, 7th of April, 2009